Need Space in PC or only want to remove or uninstall Directory printer On PC ( Windows 7, 8, 10, and Mac )? but how to, after it still having files in C: drive? If the application run on the pc, windows 7, 8, & 10 so you can uninstall using Control Panel or CMD Or If this applicaion run in Mac so you know that how to uninstall in MAC. With this article, you will able to delete or kick out all of those files also after uninstalling the Directory printer.
Are you bored, or tired of using Directory printer? Now, wanna kick-off this software from your PC ( Windows 7, 8, 10, and Mac )? There is no condition to follow up before installing, so, you can remove it without getting any confusion about it.
How to uninstall Directory printer In pc ( windows 7, 8, 10, and mac )
There are 10 methods that users can adapt if they want to uninstall Directory printer :
Method #1
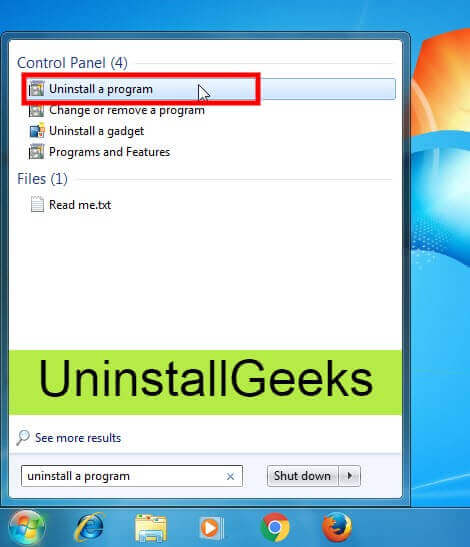
- Go to Start Menu, then click on the Control Panel.
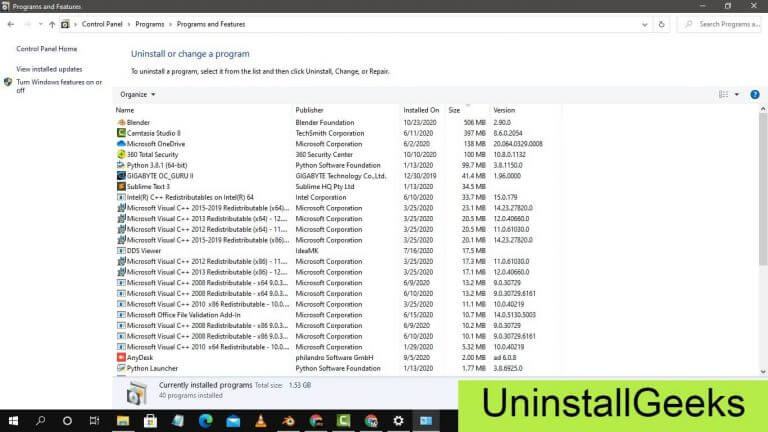
- In Control Panel, under programs, go through the list of the ones that are installed on your computer
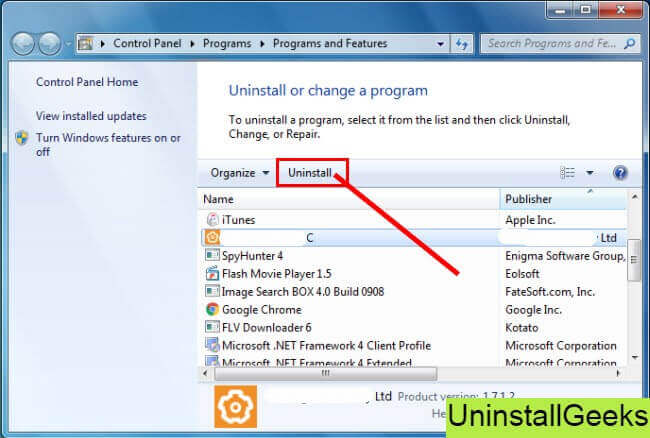
- Right-click on Directory printer, and then click on uninstall a program
- Follow the prompt on the screen, and you will get to see a progress bar that will take you to remove the Directory printer from the computer.
Method #2
The second method involves uninstaller.exe, through which Directory printer can be uninstalled. Just follow the instructions below to execute this step:
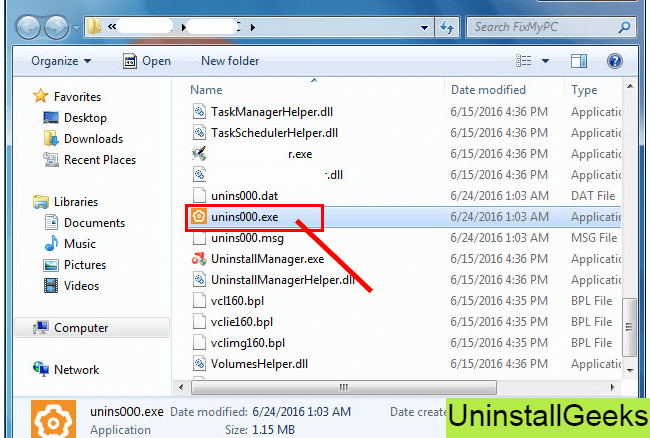
- Go to the installation folder of Directory printer.
- Find a file that is named uninstall.exe or unins000.exe
- Double click on the file, and then follow the instructions that appear on the screen.
Method #3
The third method involves System Restore. For those who don’t know, System Restore is a utility, which helps the user restore their system to its previous state. System Restore removes all those programs, which interfere with the operation and performance of the computer.
If you have created a system restore point before you installed Directory printer, then you can use this software to restore the system, and remove such unwanted programs. However, before you do so, make sure that you save all the important data.Follow the steps below to know more from this method:
- Close all the files and programs, which are currently running on your PC
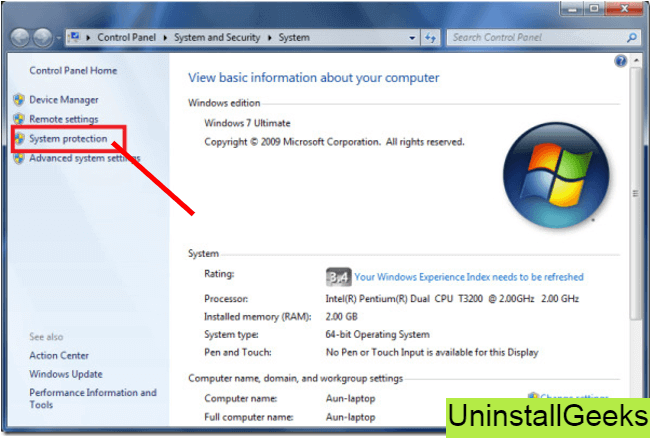
- Open Computer from the desktop, and then select Properties
- System Window will open
- On the left side and click on System Protection
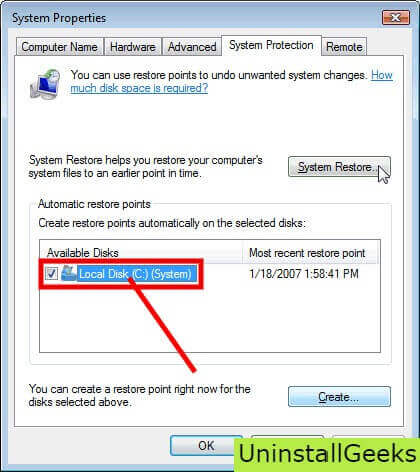
- System Properties will open.
- Then do click on the option of System Restore, and a new window will again open.
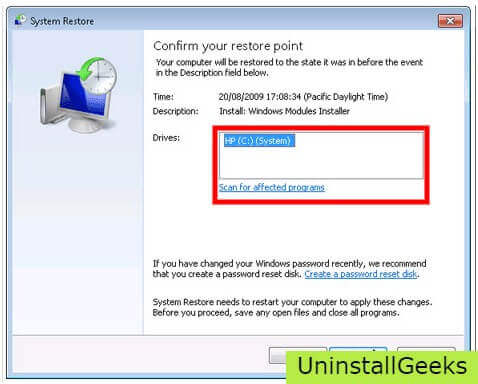
- Now, choose the ‘different restore point’ option, and click on Next.
- You have to select a date and time from the given options; when you select a date, the drivers that you installed after the chosen date won’t work.
- Click on Finish and then Confirm the ‘Restore Point’ on the screen.
- When you click Yes to confirm, the Directory printer would be uninstalled.
Method #4
If you have an antivirus, then you can use it to uninstall Directory printer.There is much malware or Directory printer software in the computer applications that we download nowadays. They have become very difficult to remove from the system, like Trojan and spyware.
- If you cannot remove Directory printer with the above methods.
- It means that there is malware or Directory printer in it, and only a good antivirus can be used for removing it.
You can either download Norton Antivirus or AVG antivirus, as these are reputable software and will surely remove the malware, Directory printer on the system. 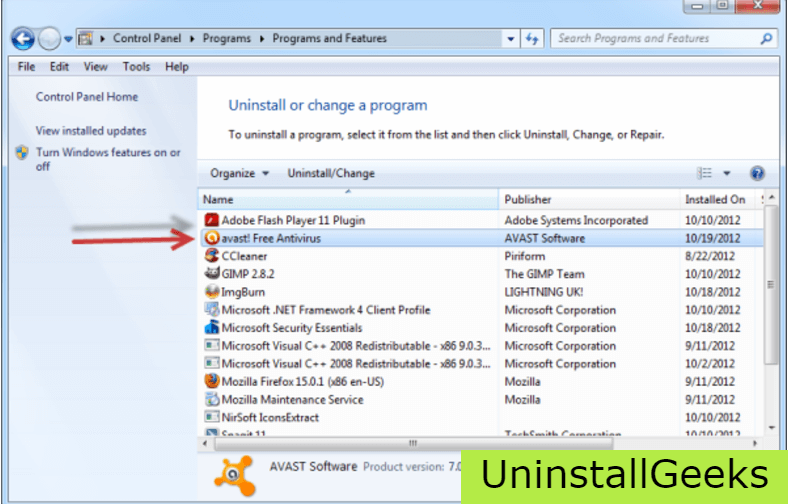
Method #5
If you want to uninstall Directory printer, then you can do so using Command Displayed in the Registry. A registry is a place where all the settings of Windows, along with information, are stored. This also includes the command to uninstall a software or program.
You can try this method with Directory printer as well, but it is a very risky method. If you make any mistake and delete the wrong information, then the system is most likely to crash. It would become difficult for you to bring it back from deletion.
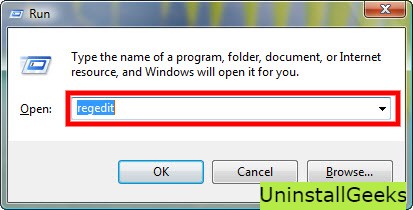
To execute this method, To follow the steps given below:
- Hold Windows + R together, and then Run command
- When the command box opens, type Regedit in the box and then click on OK
- You have to navigate and find the registry key for the Directory printer
- You will see an uninstall string on the next window; double click on it, and also copy ‘Value Data’
- Again hold Windows + R keys, and run the Command; paste the value data that you just copy and click on OK
Follow what comes on the screen and then uninstall Directory printer.
Method #6
The seventh method is to uninstall the Directory printer using a third-party uninstaller.
At times, those who don’t have any knowledge of computer language, won’t be able to manually uninstall the software fully.
Many files occupy the hard disk of the computer, so it is best to use third-party software to uninstall them.
Method #7
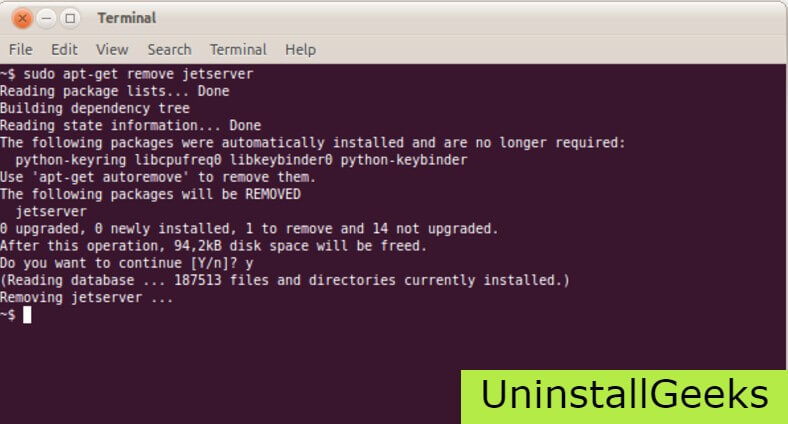
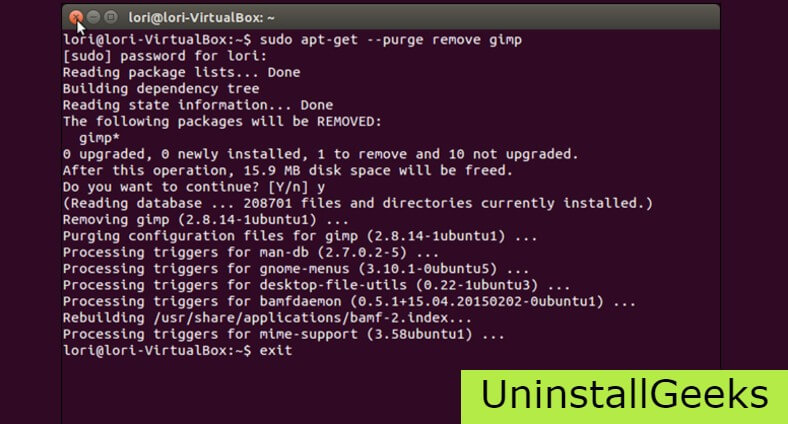
There are some codes that users can type into the command prompt, and they would be able to uninstall the Directory printer. For example, if they want to remove the package, then just type.
sudo apt-get remove Directory printer
If you want to uninstall Directory printer and its dependencies as well, then type:
sudo apt-get remove –auto-remove Directory printer
For those who don’t know, some of the dependencies of Directory printer are GCC-5, libc6, libgcc1, Directory printer dev, and gc++-5.
Method #8
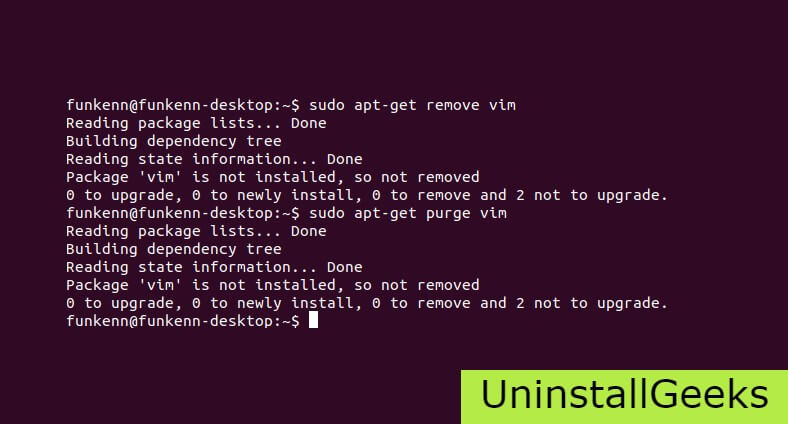
If the user wants to remove the configuration and data files of Directory printer, then they need to run the following code on the Command Prompt:
sudo apt-get purge Directory printer
Method # 9
It depends on you that are you willing to kick-out the data or you want to remove the configuration data or data files, along with the dependencies, then the following code is most likely to work for you:
sudo apt-get auto-remove -purge Directory printer
To uninstall Directory printer on mac because anytime we need space or only want to remove from pc due to some viruses and also many problems which are needed to remove or uninstall from pc.
So I will show you some steps of uninstalling Directory printer on the mac so follow my this step or method if you have still confusion so you may contact with us for uninstall of Directory printer on pc or mac.
How to Uninstall Directory printer on Mac?
For uninstalling Directory printer on the mac so as I told you that there is a simple method to uninstall apps on mac. As there are installed some apps on your Mac and now you want to remove or uninstall from your pc successfully and want to install some other apps on my mac so follow my these steps to uninstall Directory printer on mac.
Method #1
In method 1, you have to open mac on your pc as I’m showing in the image follow the images to uninstall Directory printer on your mac.
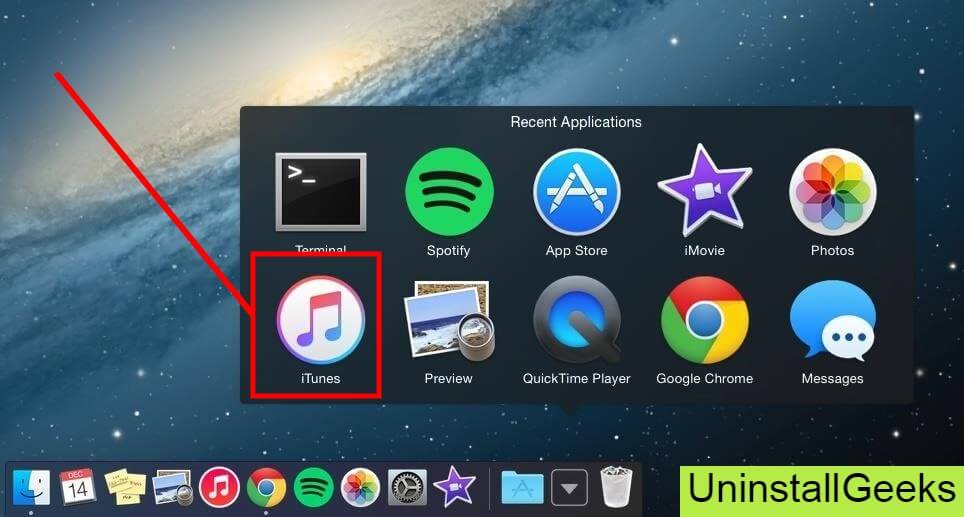
In the image, there is a Directory printer app on your mac dashboard and now we have to uninstall it from our mac we will uninstall this app and will remove it in of mac now double-click-on-app showing in the image.
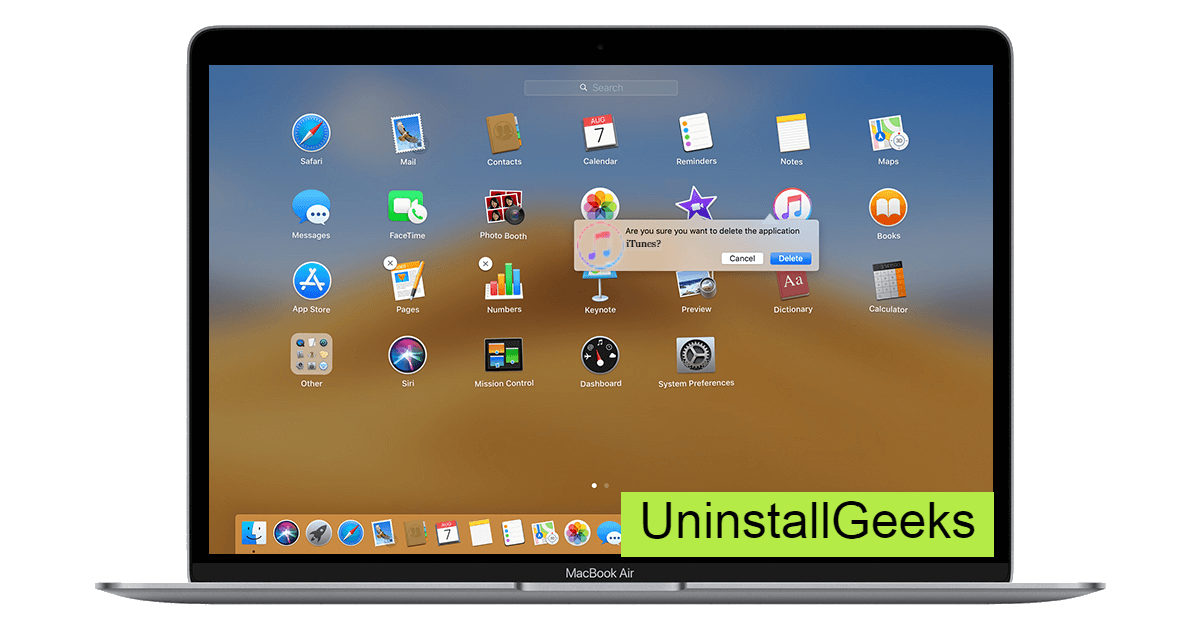
Now you double-clicked on the app mac will ask that are you sure to uninstall Directory printer click on the Delete button so go to Trash of mac to uninstall completely from mac. Showing in image trash bin click on trash bin and go inside there will be Directory printer which we had to delete before so have to uninstall completely from mac.

Not right-click on trash to remove all data or app which we had uninstalled before seeing in the image. Click on Empty Trash the whole data which is in the trash will auto remove successfully.

Now we uninstalled Directory printer on the mac so as you see that how to uninstall or remove any app on the mac so if you liked this so share once. This method doesn’t require any antivirus or uninstaller software from them we are to uninstall.
I described only a simple method of uninstalling Directory printer on mac. This method more people are using but some people take it is too hard uninstalling in mac but in this step, anyone can understand this simple method.
How To Install?
For those who don’t know much about Directory printer, they might lean more towards uninstalling it. These Directory printer create an environment, where users can create a high GPU-accelerated application. If you want to install this Directory printer, then make sure that your system is compatible with it.
Firstly, verify that the system you are using has a Directory printer capable GPU, and then download the Directory printer. Install it, and then test that the software runs smoothly on the system. If it doesn’t run smoothly, then it could be because its communication with the hardware is corrupted.
Conclusion
There are other methods of uninstalling the Directory printer as well as in pc or windows, but these could be difficult for those, who don’t have much technical expertise. Execute these methods, and they will surely work. These methods don’t require the user to have much knowledge of the technical side of an operating system. They can follow simple steps and uninstall Directory printer.